Struktur Data_Tugas Pendahuluan 3, 4 dan 5
Titik Dian Darmayanti (172355201061)
Pengertia Tree
Pengertia Tree
Tree
merupakan salah satu bentuk struktur data tidak linear yang menggambarkan
hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen.
Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus
yang disebut Root dan node lainnya. Tree juga adalah suatu graph yang acyclic,
simple, connected yang tidak mengandung loop.
Sebuah
binary search tree (bst) adalah sebuah pohon biner yang boleh kosong, dan
setiap nodenya harus memiliki identifier/value. Value pada semua node subpohon
sebelah kiiri adalah selalu lebih kecil dari value dari root, sedangkan value
subpohon di sebelah kanan adalah sama atau lebih besar dari value pada root,
masing-masing subpohon tersebut (kiri dan kanan) itu sendiri adalah juga binary
search tree.
Struktur
data bst sangat penting dalam struktur pencarian, misalkan dalam kasus
pencarian dalam sebuah list, jika list sudah dalam keadaan terurut maka proses
pencarian akan semakin cepat, jika kita menggunakan list contigue dan melakukan pencarian
biner,akan tetapi jika kita ingin
melakukan perubahan isi list (insert atau delete), menggunakan list contigue
akan sangat lambat, karena prose insert dan delete dalam list contigue butuh
memindahkan linked-list, yang untuk operasi insert atau delete tinggal
mengatur- atur pointer,akan tetapi pada n-linked list, kita tidak bisa
melakukan pointer sembarangan setiap saat, kecuali hanya satu kali dengan kata
lain hanya secara squential.
Pengertian Binary Tree
Binary
Tree merupakan salah satu bentuk struktur data tidak linear yang
menggambarkanhubungan yang bersifat hirarkis (hubungan one to many) antara
elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu
elemen khusus yang disebut Root dan node lainnya ( disebut subtree).
Dalam
tree terdapat jenis-jenis tree yang memiliki sifat khusus, diantaranya adalah
binary tree.
Binary tree adalah suatu tree dengan syarat bahwa tiap node (simpul) hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Tiap node dalam binary tree boleh memiliki paling banyak dua child (anak simpul), secara khusus anaknya dinamakan kiri dan kanan.
Binary tree merupakan himpunan vertex-vertex yang terdiri dari 2 subtree (dengan disjoint) yaitu subtree kiri dan subtree kanan. Setiap vertex dalam binary tree mempunyai derajat kluar max = 2.
Sebuah pohon biner adalah grafik asiklis
yang terhubung dimana setiap
tingkatan dari susut tidak lebih dari 3.
Ini dapat ditunjukkan bahwa dalam pohon biner manapun, terdapat persis dua atau
lebih simpul dengan tingkat satu daripada yang terdapat dengan tingkat tiga,
tetapi bisa terdapat angka apa saja dari simpul dengan tingkat dua. Sebuah
pohon biner berakar merupakan sebuah grafik yang mempunyai satu dari sudutnya
dengan tingkat tidak lebih dari dua sebagai akar.
Dengan
akar yang dipilih, setiap sudut akan memiliki ayah khusus, dan diatas dua anak bagaimanapun juga, sejauh
ini terdapat keterbatasan informasi untuk membedakan antara anak kiri atau
kanan. Jika kita membuang keperluan yang
tak terkoneksi, membolehkan bermacam
koneksi dalam komponen di grafik, kita memanggil struktur sebuah hutan.
Sebuah
jalan lain untuk mendefinisikan pohon biner melalui definisi rekursif pada
grafik langsung. Sebuah pohon biner dapat berarti :
-
Sebuah sudut tunggal.
-
Sebuah graf yang dibentuk dengan
mengambil dua pohon biner, menambahkan sebuah sudut, dan menambahkan sebuah
panah langsung dari sudut yang baru ke akar dai setiap pohon biner.
Pohon biner dapat
dikontruksi dari bahasa pemrogaraman primitif dalam berbagai cara. Dalam bahasa yang menggunakan records
dan referensi. Pohon biner secara khas dikontruksi dengan mengambil sebuah
struktur simpul pohon yang memuat beberapa data dan referensi ke anak kiri dan
anak kanan.
Kadang-kadang itu juga
memuat sebuah referensi ke ayahnya yang khas. Jika sebuah simpul mempunyai
kurang dari dua anak, beberapa penunjuk anak diaatur kedalam nilai nol khusus
atau kesebuah simpul sentinel.
Pohon biner dapat juga
disimpan sebagai struktur data implisit dalam array, dan jika pohon tersebut
merupakan sebuah pohon biner lengkap, metode ini tidak boros tempat. Dalam
penyusunan yang rapat ini, jika sebuah simpul memiliki indeks i, anaknya dapat
ditemukan pada indeks ke-2i+1 dan 2i+2, meskipun ayahnya (jika ada) ditemukan
pada indeks lantai ((i-1)/2) (asumsikan akarnya memiliki indeks kosong). Metode
ini menguntungkan dari banyak penyimpanan yang rapat dan memiliki referensi
lokal yang lebih baik, teristimewa selama sebuah preordeer traversal.
·
Istilah-istilah
dalam pohon
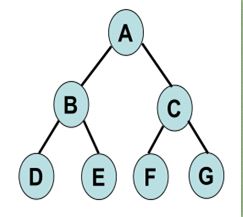
1.
Predesesor
Node yang berada diatas
node tertentu.
(contoh : B predesesor dari E dan F)
2.
Succesor
Node yang berada
dibawah node tertentu.
( (contoh : E dan F merupakan succesor dari B)
3. Ancestor
Seluruh node yang
terletak sebelum node tertentu dan terletak pada jalur
yang sama.
( (contoh : A dan B merupakan ancestor dari F)
Istilah – istilah Dalam
Pohon
4. Descendant
Seluruh node yang
terletak sesudah node tertentu
dan
terletak pada jalur yang sama.
(contoh : F dan B merupakan ancestor dari A)
5. Parent
Predesesor satu level
diatas satu node
(contoh : B merupakan
parent dari F)
6. Child
Succesor satu level
dibawah satu node
(contoh : F merupakan
child dari B)
7. Sibling
Node yang memiliki
parent yang sama dengan satu
node (contoh : E dan F
adalah sibling)
8.
Subtree
Bagian dari tree yang
berupa suatu node beserta
descendant-nya (contoh
: Subtree B, E, F dan
Subtree D, G, H)
9. Size
Banyaknya node dalam
suatu tree (contoh : gambar
tree diatas memiliki
size = 8)
10. Height
Banyaknya tingkat/level
dalam suatu tree (contoh :
gambar tree diatas
memiliki height = 3)
11. Root
(Akar)
Node khusus dalam tree
yang tidak memiliki
predesesor (Contoh : A)
12. Leaf
(Daun)
Node-node dalam tree
yang tidak memiliki daun
(contoh : Node E,F,C,G,H)
13.
Degree (Derajat)
Banyaknya
child yang dimiliki oleh suatu node
(contoh
: Node A memiliki derajat 3, node B memiliki derajat 2)
Istilah
pada pohon Binar
a.
Pohon
Biner Penuh (Full Binary Tree)
Teknik menyusuri tiap node
dalam sebuah tree secara sistematis, sehingga semua node dapat dan hanya satu kali
saja dikunjungi
Semua
simpul (kecuali daun) memiliki 2 anak dan tiap cabang memiliki panjang ruas
yang sama
b.
Pohon
Biner Lengkap (Complete Binary Tree)
Hampir sama dengan Pohon BinerPenuh, semua
simpul (kecualidaun) memiliki 2 anak tetapi tiap
cabang memiliki panjang ruas
berbeda.
c.
Pohon
Biner Similer
Dua pohon yang memiliki struktur yang sama
tetapi informasinya berbeda.
d.
Pohon
Biner Ekivalent
Dua pohon yang memiliki struktur dan informasi
yang sama.
e.
Pohon
Biner Miring (Skewed Tree)
Dua pohon yang semua simpulnya mempunyai satu
anak / turunan kecuali daun.
Sifat utama Pohon Berakar
1.
Jika Pohon mempunyai Simpul sebanyak n, maka banyaknya ruas
atau edge adalah (n-1).
2.
Mempunyai Simpul Khusus yang disebut Root, jika Simpul
tersebut memiliki derajat keluar >= 0, dan derajat masuk = 0.
3.
Mempunyai Simpul yang disebut sebagai Daun / Leaf, jika
Simpul tersebut berderajat keluar = 0, dan berderajat masuk = 1.
4.
Setiap Simpul mempunyai Tingkatan / Level yang dimulai dari
Root yang Levelnya = 1 sampai dengan Level ke - n pada daun paling bawah.
Simpul yang mempunyai Level sama disebut Bersaudara atau Brother atau
Stribling.
5. Pohon
mempunyai Ketinggian atau Kedalaman atau Height, yang merupakan Level tertinggi
6. Pohon
mempunyai Weight atau Berat atau Bobot, yang banyaknya daun (leaf) pada Pohon.
7. Banyaknya
Simpul Maksimum sampai Level N adalah :
2
(N) - 1
|
8. Banyaknya
Simpul untuk setiap Level I adalah :
N
∑ 2 ( I – 1)
I
= 1
|
Kunjungan
pada pohon Biner
Kunjungan
pohon biner terbagi menjadi 3 bentuk
binary tree :
1. Kunjungan secara preorder ( Depth First Order), mempunyai urutan :
1. Kunjungan secara preorder ( Depth First Order), mempunyai urutan :
a. Cetak
isi simpul yang dikunjungi ( simpul akar ),
b. Kunjungi
cabang kiri,
c. Kunjungi
cabang kanan .
2.
Kunjungan secara inorder ( symetric
order), mempunyai urutan :
a. Kunjungi cabang kiri,
a. Kunjungi cabang kiri,
b. Cetak isi simpul yang dikunjungi (simpul
akar),
c. Kunjungi
cabang kanan .
3. Kunjungan
secara postorder, mempunyai urutan :
a. Kunjungi cabang kiri,
b.
Kunjungi cabang kanan,
c.
Cetak isi simpul yang dikunjungi ( simpul akar ).
Aplikasi
pohon Biner
Notasi
Prefix, Infix dan Postfix
Pada bagian ini akan
dibahas tentang bagaimana menyusun sebuah Pohon Binar yang apabila
dikunjungisecara PreOrder akan menghasilkan Notasi Prefix,kunjungan secara
InOrder menghasilkan Notasi Infix, dankunjungan PostOrder menghasilkan Notasi
Postfix.
Tree Traversal
Ada tiga cara traversal
preorder
inorder
postorder
Untuk tree yang kosong,
traversal tidak perlu dilakukan
1. Preorder (SLR)
- Simpul / Node nya
- Subtree sebelah kiri (Left)
- Subtree sebelah kana (Right)
Contoh :
Implementasi dalam bahasa C
struct node {
struct
node *left;
struct
node *right;
char
label;
}
void preorder(struct
node *p)
{
if
(p==NULL) return; jika empty-tree,
tidak perlu lakukan
printf(“visit
%c ”, p->label); tampilkan label node yang dikunjungi
preorder(p->left); traverse
the left subtree
preorder(p->right); traverse the right subtree
}
2. Inorder (LSR)
- Subtree sebelah kiri (Left)
- Simpul / Node nya
- Subtree sebelah kana (Right)
contoh :
Implementasi dalam bahasa C
struct node {
struct
node *left;
struct
node *right;
char
label;
}
void inorder(struct
node *p)
{
if
(p==NULL) return; jika empty-tree,
tidak perlu lakukan
inorder(p->left); traverse
the left subtree
printf(“visit
%c ”, p->label); tampilkan label node yang dikunjungi
inorder(p->right); traverse the right subtree
}
3. Postorder (LRS)
- Subtree sebelah kiri (Left)
- Subtree sebelah kana (Right)
- Simpul /Node nya
contoh :
Implementasi dalam bahasa
C
struct node {
struct
node *left;
struct
node *right;
char
label;
}
void postorder(struct
node *p)
{
if
(p==NULL) return; jika empty-tree,
tidak perlu lakukan
postorder(p->left); traverse
the left subtree
postorder(p->right); traverse the right subtree
printf(“visit
%c ”, p->label); tampilkan label node yang dikunjungi
}
Contoh Preorder, Postorder, Inorder















Komentar
Posting Komentar